App-specific configurations

For simple use-cases, tuning Espanso's options in the config/default.yml file works well, but as your needs become more complex, that mechanism might prove limited. For example, you might want to customize the way Espanso behaves while using a certain app, or disabling it entirely when using another.

App-specific configurations are designed to handle these use-cases. In a nutshell, they are made of two important ingredients:

• Some rules that define when the configuration should be active
• The actual configuration options

Wayland

App-specific configurations are not yet supported in Wayland.

Disabling Espanso when using a certain app

Let's start with a simple example. Let's say we would like to disable Espanso while using Telegram. To do so, we'll create an app-specific configuration. Start by creating the config/telegram.yml file, with the following content:

$CONFIG/config/telegram.yml

filter_exec: Telegram
enable: false

Let's analyze the configuration step by step:

• We first specify the filter_exec rule, which defines when this app-specific config will be active. In this case, the configuration will be active if the current app's executable path contains the string "Telegram". You'll learn all about available filters in the Filters section.

• We then set enable: false, disabling Espanso.

Espanso will now use the configuration defined in the config/telegram.yml file while using Telegram and the default one while using other applications.

Inside the app-specific configuration you can define most of the options you would customize in your config/default.yml file, with a few exceptions. You'll find a list of customizable options in the Options section.

Enable or disable some matches while using a specific application

Another common use-case for app-specific configurations is to selectively enable some matches while using a particular application. For example, we might want to enable some code snippets while using Visual Studio Code or IntelliJ Idea, but not inside other apps.

This use-case is described in the Include and Exclude rules section.

Understanding configuration inheritance

App-specific configurations extend the default one. For example, if your config/default.yml file defines option_A: 10 and option_B: 20, and your app-specific configuration config/specific.yml defines option_B: 30, the latter will be equivalent to:

option_A: 10
option_B: 30

The option_A parameter was inherited by the default configuration, as shown in this schema:

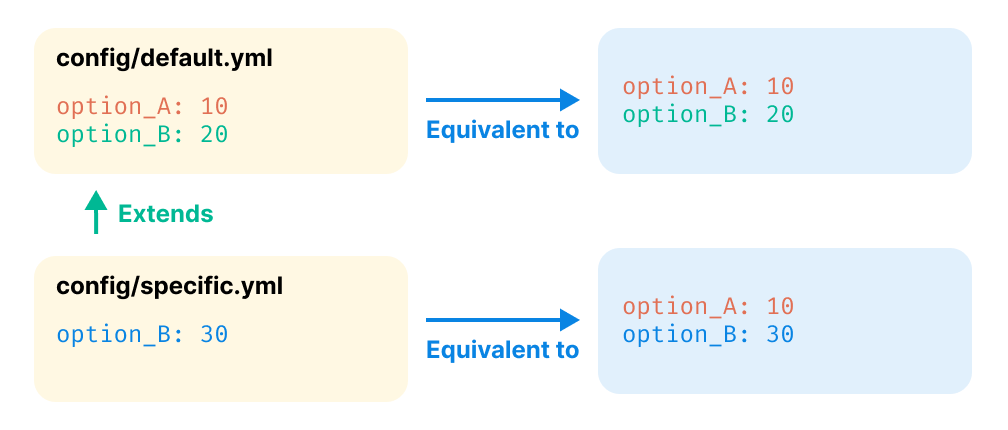
The key concept to remember is that the app-specific configuration will be equivalent to the default one, except for the options it changes directly.

tip

Espanso's currently active configuration for a program can be shown in a popup window by typing #acfg# from within it. Similarly, #pacfg# will paste the details into the program so use with care!

Filters

As said earlier, one of the key ingredients for app-specific configurations are the filtering rules. These determine which configuration is active at any given time.

These are the currently available filters:

Filter	Description	Windows Support	MacOS Support	Linux Support
filter_title	Filter based on the current window title.	Full support	Full support	Full support
filter_exec	Filter based on the current application's executable path. For example, C:\Programs\Telegram.exe	Full support	Full support	Partial support
filter_class	Filter based on the current window class. This is mostly relevant on Linux	Uses the application executable path instead	Uses the App identifier instead	Full support

Additionally, filter_os, accepts as a parameter linux, macos or windows, and may be usefully combined with extra_includes to separate OS-specific global variables and local shell expansions etc., when the Espanso configuration files are shared between different operating systems.

Note that, in addition to default.yml, only one app-specific configuration can apply at any time. In situations where more than one filter could apply to the same program (e.g. a browser filter, and a tab filter) the first one alphanumerically by file-name will be active. Name the filter files accordingly so that, in the example, a filter_title file overrides a more general filter_exec file.

Filter values match by regex, so ensure that character case is consistent and special characters are properly escaped.

For example, if the current app title is Google Chrome:

• filter_title: Chrome will match, as the string Google Chrome matches the regex Chrome
• filter_title: "^Chrome$" will NOT match, as that regex matches only an app with the title equal to Chrome.
• filter_title: "^Google Chrome$" will match, as the string Google Chrome exactly matches the regex Google Chrome.

Use of the regex alternation operator (|) makes it possible to share configurations between programs, e.g.:

filter_class: libreoffice-writer|VSCodium
backend: clipboard

Finding the right filters

tip

The method described below requires Espanso v2.1.1 or above, so make sure you have an up-to-date version.

Now that we covered the basics, let's discuss how to choose the right filter for your use-case.

We should start by checking what information Espanso is detecting for the current application, as that's what Espanso will use in the matching phase.

1. Open the desired application (in this example, I've opened the macOS's TextEdit app).
2. Inside the application, type #detect#
   • As an alternative, you can also open the Search bar, type > and then select Show active application information (detect)
3. A window should open, displaying the information about the active application:

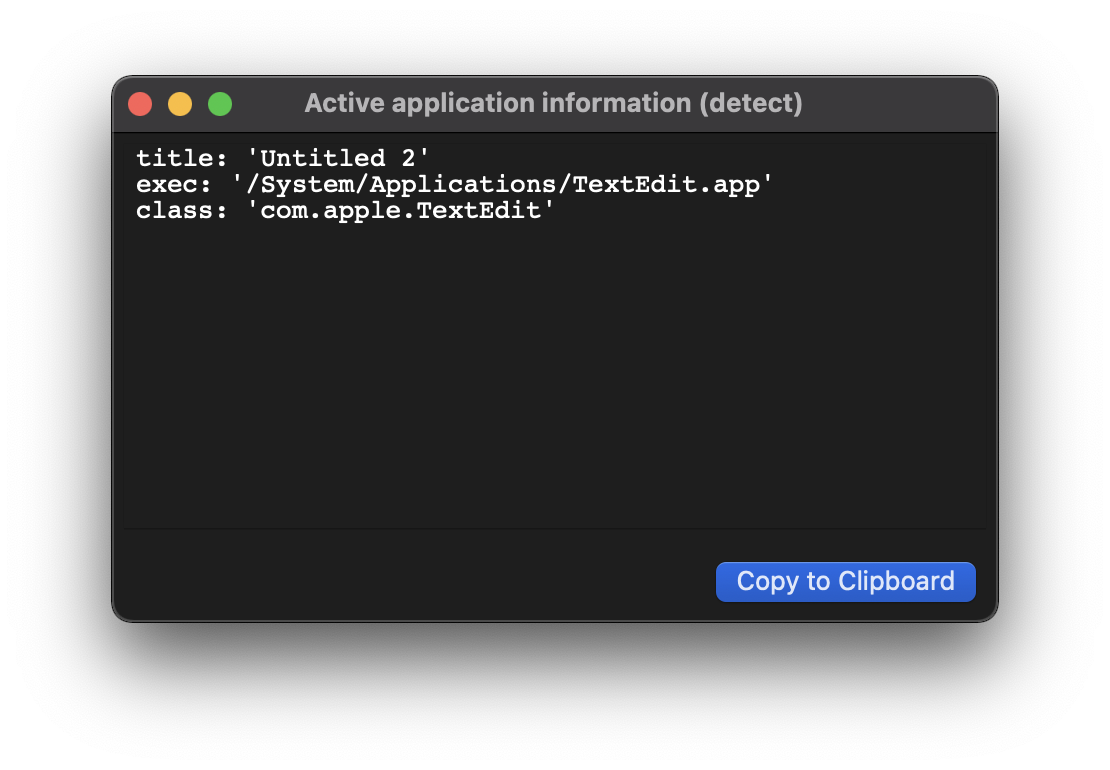
#pdetect# can be used to paste the information directly into your application.

These are the values of title, exec and class detected for the active application.

In this example, a good filter could be:

filter_class: "TextEdit"

Which would match against the detected class com.apple.TextEdit.

A good rule of thumb is to choose either the filter_exec or filter_class filters for basic use-cases, as these values tend to be stable. In the next section, we'll discuss an interesting use-case for filter_title.

Filters are often platform-dependent

If you are sharing your configuration across different machines, an important consideration to make is that the same filters might not work across different operating systems.

For example, if you define a filter_exec as follows:

filter_exec: Telegram.exe

That would match Telegram on Windows, but not on macOS or Linux. To solve the problem, you can either create filters that match all the possible app locations/classes (filters are regexes, so you can also use alternation) or you can create different app-specific configurations based on the platform, such as config/telegram_win.yml and config/telegram_linux.yml.

Advanced use-cases for filter_title

As mentioned in the previous section, filter_title is trickier to use than filter_class and filter_exec, as its value is not stable over time. The value often reflect the content being displayed in the active application:

• Inside a browser, the title might be the webpage title. For example, if you are visiting YouTube inside Chrome, the title is either YouTube or the video title.
• Inside an editor, the title might refer to the file being edited. For example, while editing this documentation file inside Visual Studio Code, the detected title is app-specific-configurations.md - website-espanso - Visual Studio Code.

This opens up a few interesting use-cases. For example, you might create an app-specific configuration that only activates when visiting a particular website, or one that would only activate while editing a specific project/document.

For example, here's a configuration that would disable Espanso when the active page is YouTube:

config/disable_on_youtube.yml

filter_title: YouTube
enable: false